Chapter 2.1 - 2.4

Reading mathematical expressions

Common expressions

Difference
$| x - 5 | \leq 6$ - the distance between x and 5 is less or equal to 6
$x \in [- 1, 11]$
$| x + 5 | > 6$ - the distance between x and -5 is greater than 6
$x \in (- \infty, - 1) \cup (11, + \infty)$
Summation
$\sum_{i = 1}^{n} t_{i} = t_{1} + t_{2} + \dots + t_{n - 1} + t_{n}$
$\sum_{i = 2}^{5} i^{2} = 2^{2} + 3^{2} + 4^{2} + 5^{2} = 4 + 9 + 16 + 25 = 54$

Variables

$n$ - sample size
$N$ - population size
$μ$ - population mean
$\bar{x}$ - sample mean

Proportions

A proportion is the percentage of observations/data values that have a certain characteristic

A sample statistic: $\hat{p} = \frac{# observations}{n}$ , where $n$ is the sample size
A population parameter: $p = \frac{# observations}{N}$ , where $N$ is the population size

Proportions of types of variables

Nominal - how many people are in grad school
Ordinal - how many people got first place
Interval - values between $X$ and $Y$
Ratio - is $1 / 3^{r d}$

Variable classification

Identify the variables for which proportions are calculated
Classify the level of measurement for proportion
Caution: care must be taken when making comparisons with proportions across different data sets

Distributions

Descriptive statistics summarize without painting a full picture

Distributions and visualizations show us a glimpse of the data as a whole, but often fail to paint a full picture

Best practice

When analyzing data, create distributions and visualizations to develop a sense of data

Distribution components

A distribution segments all of the data into classes that are exhaustive, mutually exclusive, and equal length

Distribution provides information about the number of data values in each class.
Frequency disctributions provide raw count in each class
Relative frequency distributions provide the proportion of values in each class

Example drawing

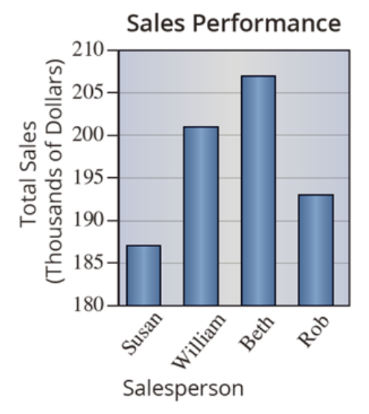
Classes - 4, each for one person

Important to note

The graph starts at 180, so ratios look much bigger than in reality

!!!Comparing bar height is different than comparing sales performance!!!

Fixed bar graph

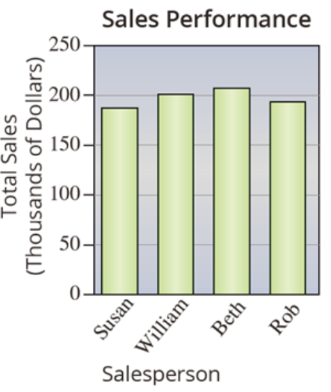
Naming

Space in between bars - bar graph
No space in between bars - histogram

Norms for visualization

Use histograms for continuous quantitative variables
Use bar graphs for qualitative and discrete variables

For interval variables, indicate the level and caution making ration comparisons
For ratio variables, have vertical axis start at zero
if not at zero, the variable is rendered as interval
Communicate clearly

Box plots

Define four classes so that each class has approximately same proportion of observations
it might not be possible to split population in 4 equal classes due to the population size not being divisible

Quartiles

First quartile $Q_{1}$ - a value at which 25% of data values are less or equal to the value
Second quartile $Q_{2}$ - a value at which approximately 50% of data values are less or equal to the value
First quartile $Q_{3}$ - a value at which 75% of data values are less or equal to the value

To have four classes, we need 5 boundary points. The other two are:

Sample minimum
Sample maximum

Quartile computation

Sort data values in ascending order
Determine how many observations will need to be less than or equal to the value. We call this the rank
If the found rank is an whole integer, we use $R = \frac{x_{R^{'}} + x_{R^{'} + 1}}{2}$
Find the smallest value that is smaller or equal than the value at rank

Example
data set - ${17, 52, 76, 76, 81, 90}$
size - $n = 6$
quartile 1:
rank - $R_{1} = 0.25 \cdot 6 = 1.5 \to 2$
$Q_{1} = 52$
quartile 2:
rank - $R_{2} = 0.5 \cdot 6 = 3$
$Q_{2} = \frac{76 + 76}{2} = 76$
taking 3 values, we can see that there is 76 before and after the rank, so we have to use a bit different computation. This is the reason for "approximately" in the definition
quartile 3:
rank - $R_{3} = 0.75 \cdot 6 = 4.5 \to 5$
$Q_{3} = 81$
min: 17
max: 90
Example

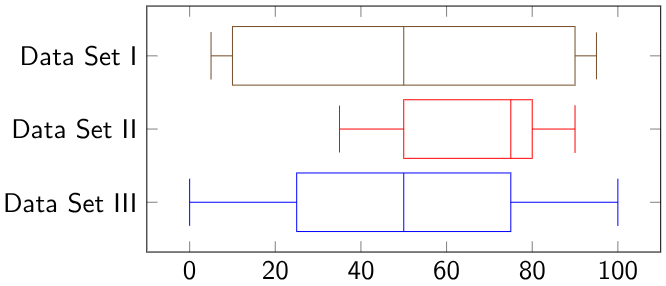
Which set has the greatest proportion of values greater than 50?
Data set II
Which set has the largest value? - Data set III
Which set has the smallest box? - Data set II
Size of the box - inter-quartile range
Which set has the greatest number of values above 80?
we cannot say, as the boxes show percentages, and not where the values are on the plot
Which set has the most tightly packed data - we can't say
Which set is the most symmetric - we can't say

Percentiles

We use percentiles to generalize quartiles
The third quartile is value such that approx. $75 %$ of data values are less or equal than the q.value. The same goes for other quartiles

Percentiles allow us to specify any percentage between 0 and 100

The percentile is calculated exactly like the quartile
$81^{s t}$ percentile:
Rank - $R = 0.81 \cdot 6 = 4.86 \to 5$
$81^{s t}$ = 81 (which is actually equal to the $Q_{3}$ )

Examples

1 - $81^{s t}$ of the first 200 positive, even numbers
$R = 0.81 \cdot 200 = 162$
$162^{n d}$ value - 324
$163^{n d}$ value - 326
$81^{s t} = \frac{324 + 326}{2} = 325$
2 - construct a data set with indicated size and Five Number Summary
a) n = 6, min = 1, $Q_{1} = 4$ , $Q_{2} = 5$ , $Q_{3} = 7$ , max = 10
$R_{1} = 0.25 \cdot 6 = 1.5 \to 2$
$R_{2} = 0.5 \cdot 6 = 3$
$R_{3} = 0.75 \cdot 6 = 4.5 \to 5$
{1, 4, 4, 6, 7, 10}
b) n = 7, min = 100, $Q_{1} = 108$ , $Q_{2} = 122$ , $Q_{3} = 125$ , max = 126
$R_{1} = 0.25 \cdot 7 = 1.75 \to 2$
$R_{2} = 0.5 \cdot 7 = 3.5 \to 4$
$R_{3} = 0.75 \cdot 7 = 5.25 \to 6$
{100, 108, 110, 122, 124, 125, 126}
c) n = 8, min = -1, $Q_{1} = 0$ , $Q_{2} = 5$ , $Q_{3} = 5$ , max = 15
$R_{1} = 0.25 \cdot 8 = 2$
$R_{2} = 0.5 \cdot 8 = 4$
$R_{3} = 0.75 \cdot 8 = 6$
{-1, 0, 0, 5, 5, 5, 5, 15}
3 - construct a data set with 15 entries so that the $34^{t h} = 50$ , $73^{r d} = 84$
$R_{34} = 0.34 \cdot 15 = 5.1 \to 6$ $34^{t h} = 50$
$R_{73} = 0.73 \cdot 15 = 10.95 \to 11$ $73^{t h} = 84$
{1, 2, 3, 4, 5, 50, 51, 52, 53, 54, 84, 85, 86, 87, 88}
4 - What is the smallest size of set so that it has different values for each whole number percentile between $31^{t h}$ and $40^{t h}$ ?
Using excel - 93