AC Power

Instantaneous power

$p (t) = u (t) \times i (t)$
$i (t) = I_{m} \cos (ω t + ϕ)$
$u (t) = U_{m} \cos (ω t + ψ)$

p (t) = I_{m} U_{m} \cos (ω t + ϕ) \cos (ω t + ψ) = \frac{1}{2} I_{m} U_{m} (\cos (ϕ - ψ) + \cos (2 ω t + ϕ + ψ))

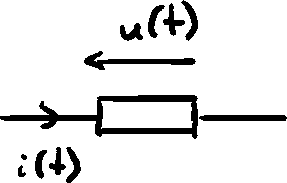
Mean power

\begin{aligned} P = \frac{1}{T} \int_{t_{0}}^{t_{1} + T} p (t) d t, & T = \frac{2 π}{ω} \end{aligned}

In AC, mean power is also called real power
If $p (t) = \frac{1}{2} U_{m} I_{m} (\cos (ϕ - ψ) + \cos (2 ω t + ϕ + ψ))$ , then $P = \frac{1}{2} U_{m} I_{m} \cos (ϕ - ψ)$

Examples

Inductor - $P = 0$
Capacitor - $P = 0$
Resistor - $P = \frac{1}{2} | I |^{2} R = \frac{1}{2} \frac{| U |^{2}}{R}$

Root Mean Square

X_{R M S} = \sqrt{\frac{1}{T} \int_{t_{0}}^{t_{0} + T} x^{2} (t) d t}

For harmonic signal $x (t) = X_{m} \cos (ω t + ϕ)$

X_{R M S} = \frac{X_{m}}{\sqrt{2}}

Real power and RMS

$P = \frac{1}{2} | I |^{2} Re (Z) = \frac{1}{2} | U |^{2} Re (\frac{1}{Z})$
$P = I_{R M S}^{2} Re (Z) = U_{R M S}^{2} Re (\frac{1}{Z})$
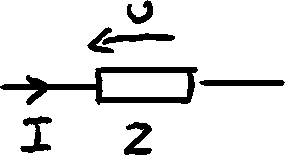
for resistor Z=R, we obtain "the same" formulas as for DC
$P = I_{R M S}^{2} R = \frac{U_{R M S}^{2}}{R}$

Maximum Power Transfer theorem

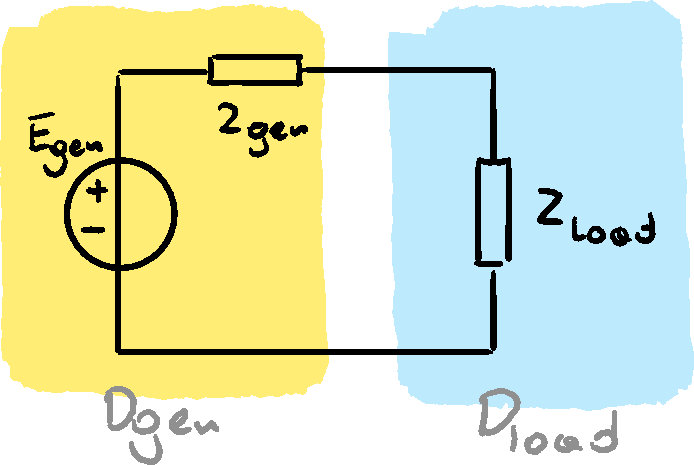
If $E_{g e n} = 0$ and $Z_{g e n}$ are const, and $Re (Z_{g e n}) > 0$ , then the maximal real power that can be transferred to $Z_{l o a d}$ is equal to

P_{m a x} = \frac{| E_{g e n} |^{2}}{8 Re (Z_{g e n})}

Such power is delivered to $Z_{l o a d}$ iff $Z_{l o a d} = \overset{―}{Z_{g e n}}$