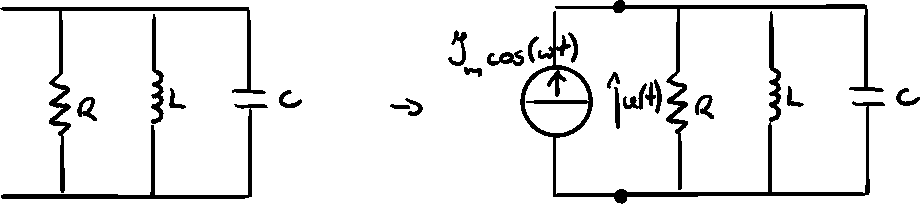Resonance

A resonant pulsation of one port is ${\omega }_0$ such that $|Z(\omega )|$ attains at $w_0$ a proper local minimum or maximum

Resonant pulsation is a ${\omega }_0$ for which impedance becomes purely real
${\omega }_0=2\pi f_0$

Q factor

Q factor related to resonant pulsation is

where $\omega (0,T)$ is energy transferred to one-port in $T$, and $W_{max}$ is maximal (over $T_0$) value of energy stored

Series Resonant Circuit (SRC)

$Z(\omega )=R+j\omega L+\frac{1}{j\omega C}=R+j(\omega L-\frac{1}{\omega C})$
$|Z(\omega ){|}^2=R^2+{(\omega L-\frac{1}{\omega C})}^2=R^2-2\frac{L}{C}+{\omega }^2{L}^2+\frac{1}{{\omega }^2{C}^2}$
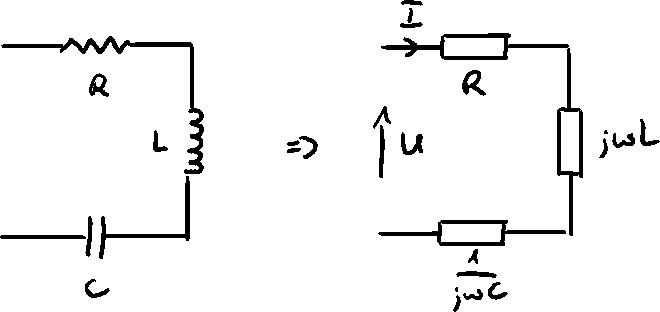
$0=\frac{d|Z{|}^2}{d\omega }({\omega }_0)$, so $0=2L^2{\omega }_0-\frac{2}{{\omega }_0^3{C}^2}\to {\omega }_0=\frac{1}{\sqrt{LC}}$
$Z(\omega )=R+j(\omega L-\frac{1}{\omega C})=R+\frac{1}{\omega C}j({\omega }^{2}LC-1)\underset{{\omega }_0=\frac{1}{\sqrt{LC}}}{=}R+\frac{1}{\omega C}j(1-1)=R+0=R$
$Q=\frac{2\pi W_{max}}{\omega (0,T)}$

Real power

$P_w=\frac{1}{2}|I{|}^2\mathrm{Re}(Z(\omega ))$, so $\omega (0,T)=\frac{\pi }{{\omega }_0}|I{|}^{2}R$
$W_{max}=\frac{1}{2}max(L{i}_L^2(t)+C{u}_C^2(t))=\frac{|I{|}^2}{2{\omega }_0^{2}C}$
and finally
$Q=\frac{1}{{\omega }_{0}RC}=\frac{\sqrt{\frac{L}{C}}}{R}\rho =\sqrt{\frac{L}{C}}\leftarrow$ characterisctic resistance of SRC

Absolute detuning

For SRC, absolute detuning related tu pulsation $\omega$ is defined as ${\xi }_{\omega }=(\omega L-\frac{1}{\omega C})\frac{1}{R}$

Filtration

For resonant pulsation ${\omega }_0({\xi }_{\omega }=0)$, $i(t)=\frac{E_m}{R}\cos ({\omega }_{0}t)$

$U_R(t)=E_m\cos ({\omega }_{0}t)$
$U_L(t)=Q{E}_m\cos ({\omega }_{0}t+\frac{\pi }{2})$
$U_L(t)=Q{E}_m\cos ({\omega }_{0}t-\frac{\pi }{2})$

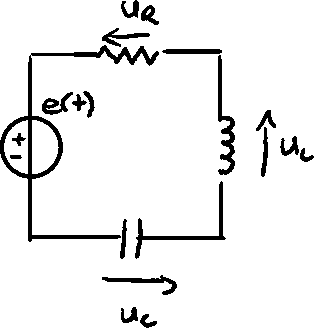
Relative pulsation related to pulsation $\omega$ is
${\nu }_w=\frac{\omega }{{\omega }_0}-\frac{{\omega }_0}{\omega }$, and so ${\xi }_{\omega }=Q_{\nu }$

Parallel resonant circuit (PRC)

$Y(\omega )=\frac{1}{R}+\frac{1}{j\omega L}+j\omega C=\frac{1}{R}(1+jR(\omega C-\frac{1}{\omega L}))$
$Z_{\omega }=\frac{R}{1+j{\xi }_{\omega }}$
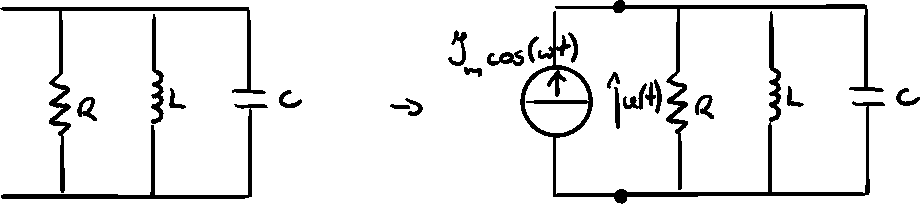
$Q=\frac{R}{{\omega }_{0}L}={\omega }_{0}RC=\frac{R}{\sqrt{LC}}\rho =\sqrt{\frac{L}{C}}\leftarrow$ characteristic resistance of PRC

Absolute detuning ${\xi }_{\omega }=R(\omega C-\frac{1}{\omega L})$
Relative detuning ${\nu }_{\omega }=\frac{\omega }{{\omega }_0}-\frac{{\omega }_0}{\omega }\to \xi =Q\nu$
Current resonance (for $\omega ={\omega }_0$) - $u(t)=I_{m}R\cos ({\omega }_{0}t)$

$i_r(t)=I_m\cos ({\omega }_{0}t)i_L(t)=Q{I}_m\cos ({\omega }_{0}t-\frac{\pi }{2})i_C(t)=Q{I}_m\cos (\omega t+\frac{\pi }{2})$