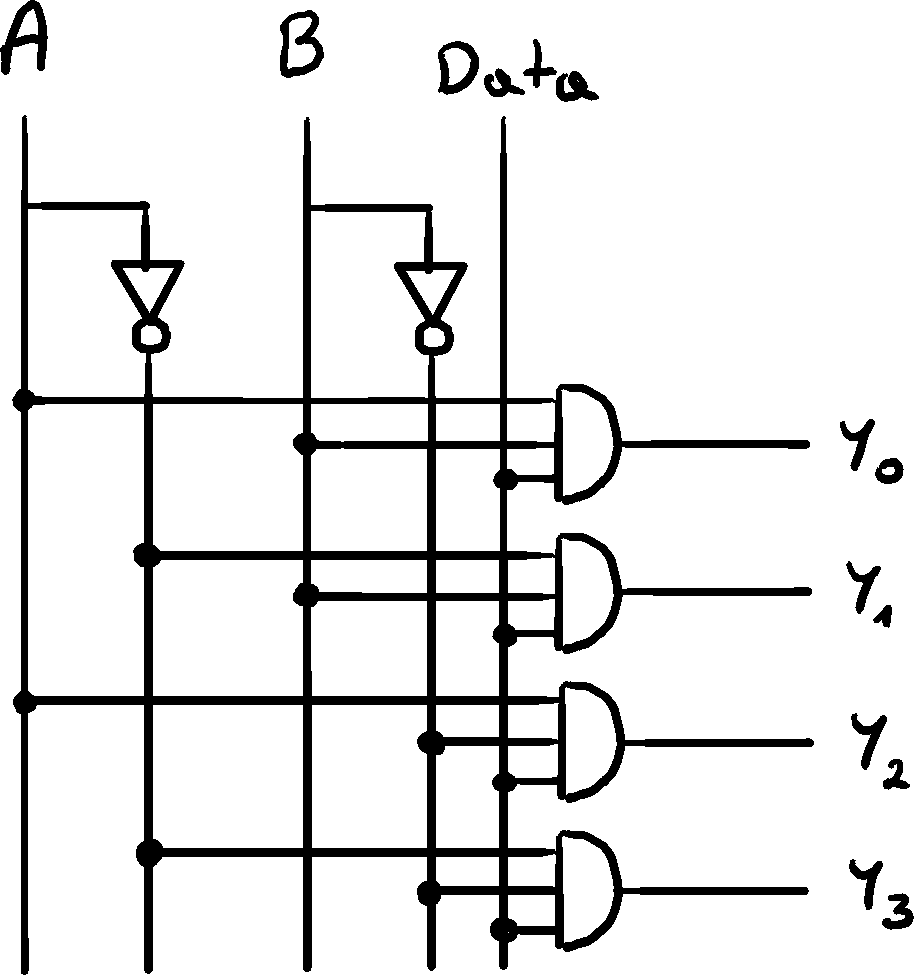
Combinatorial Logic

Multiplexers

MUX2

Let $x_a,x_b$ be address inputs and $x_c,x_d,x_e$ be data inputs
$y=\overline{x_a}\overline{x_b}{f}_y(0,0,x_c,x_d,x_e+x_e)+\overline{x_a}{x}_b{f}_y(0,1,x_c,x_d,x_e)+$
$x_a\overline{x_b}{f}_y(1,0,x_c,x_d,x_e)+x_a{x}_b{f}_y(1,1,x_c,x_d,x_e)$

$f_y(0,0,x_c,x_d,x_e)=x_e$
$f_y(0,1,x_c,x_d,x_e)=0$
$f_y(1,0,x_c,x_d,x_e)=\overline{x_d}{x}_e$
$f_y(0,0,x_c,x_d,x_e)=x_c+\overline{x_d}{x}_e+x_d\overline{x_e}=x_c+(x_d\oplus x_e)$

$a\overline{d}e=a\overline{b}\overline{d}e+ab\overline{d}e$

For $A_0=b$
$D_0=\overline{d}e$
$D_1=\overline{d}e+c+d\overline{e}=c+d+e$

We can convert it into a MUX4

MUX3

let $x_a,x_b,x_e$ be address inputs and $x_c,x_d$ data inputs


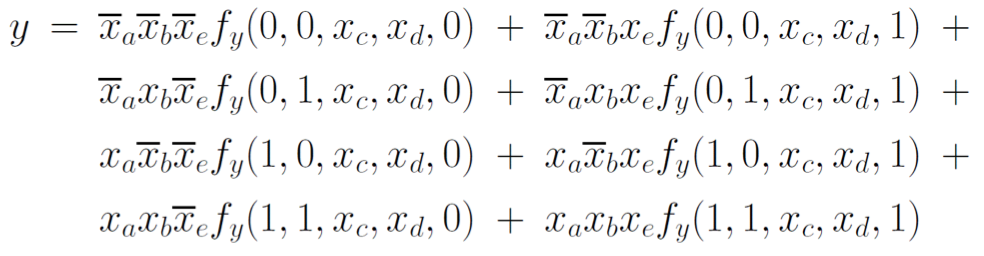
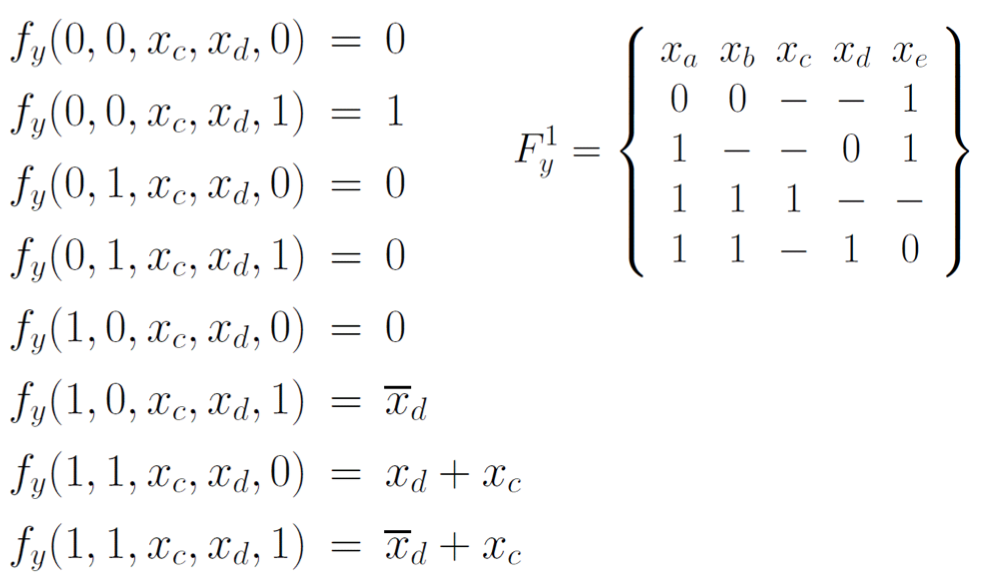
This can be turned into this circuit

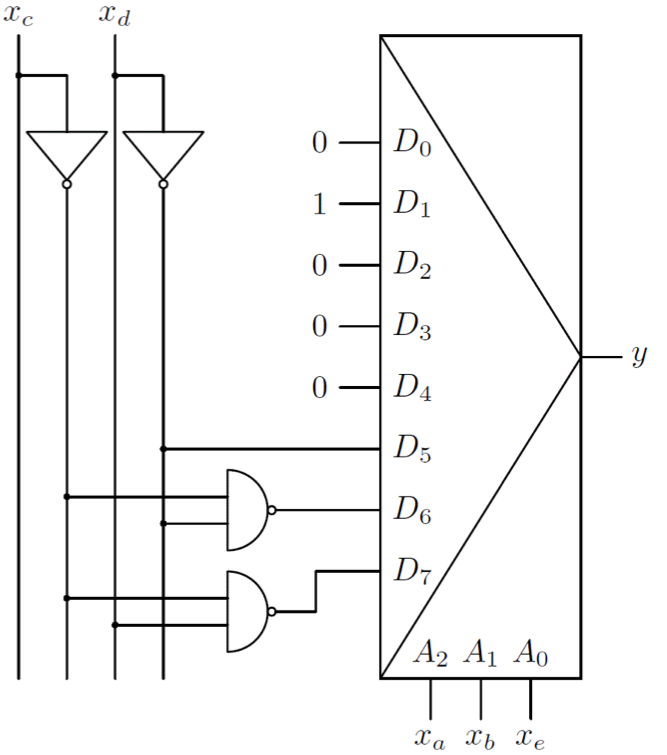
MUX4

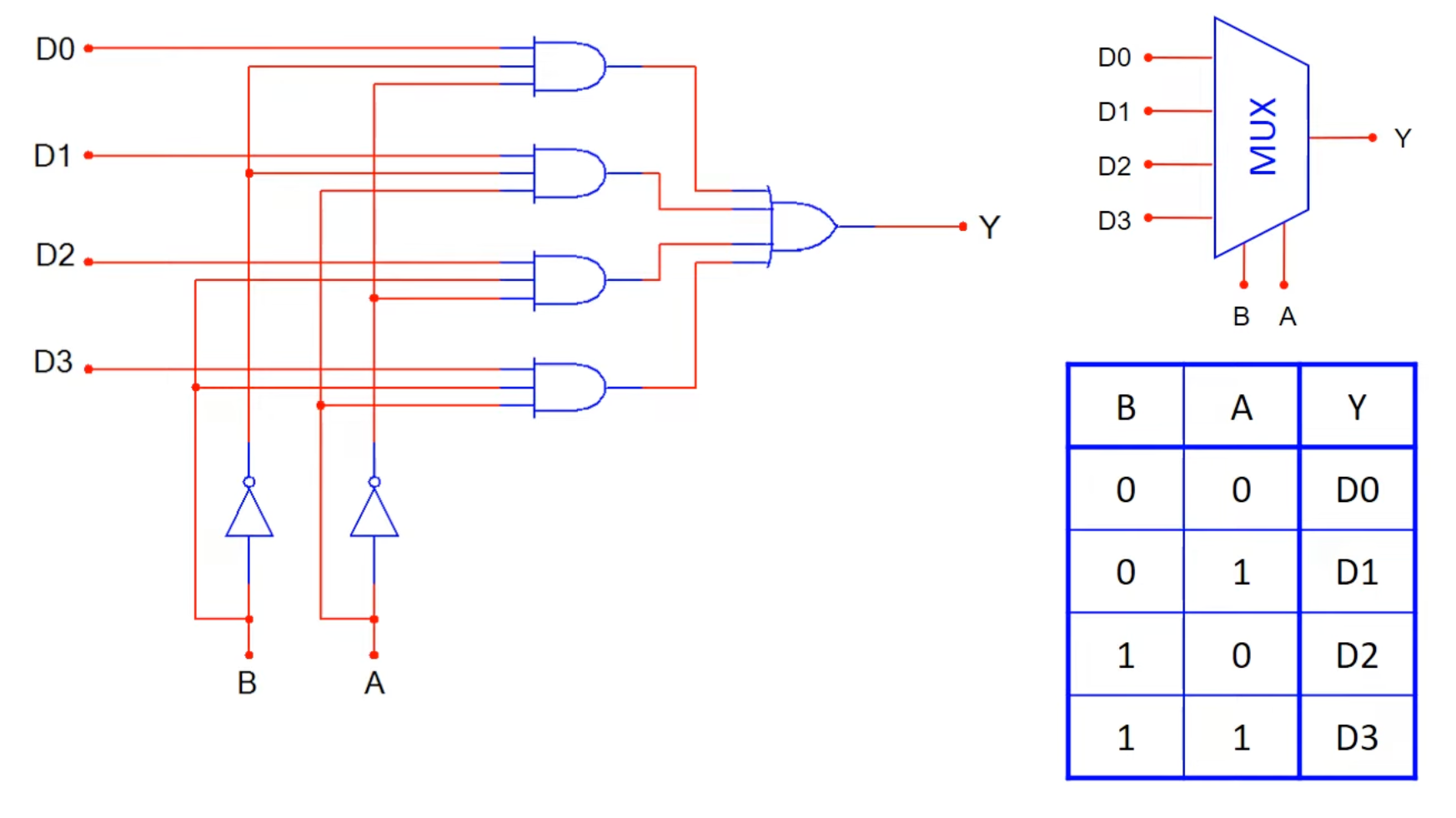
Example 1

this turned into

and shown as

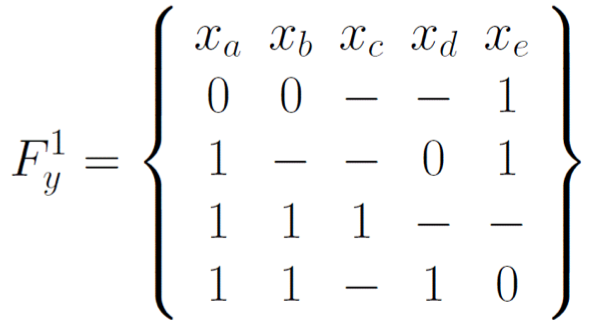
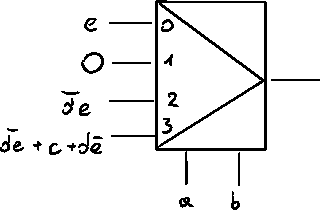
Now we choose $x$'s with least DONTCARE as address inputs ($x_a,x_b.x_d,x_e$) and $x_c$ becomes a data input. Which turns into this beautiful mess

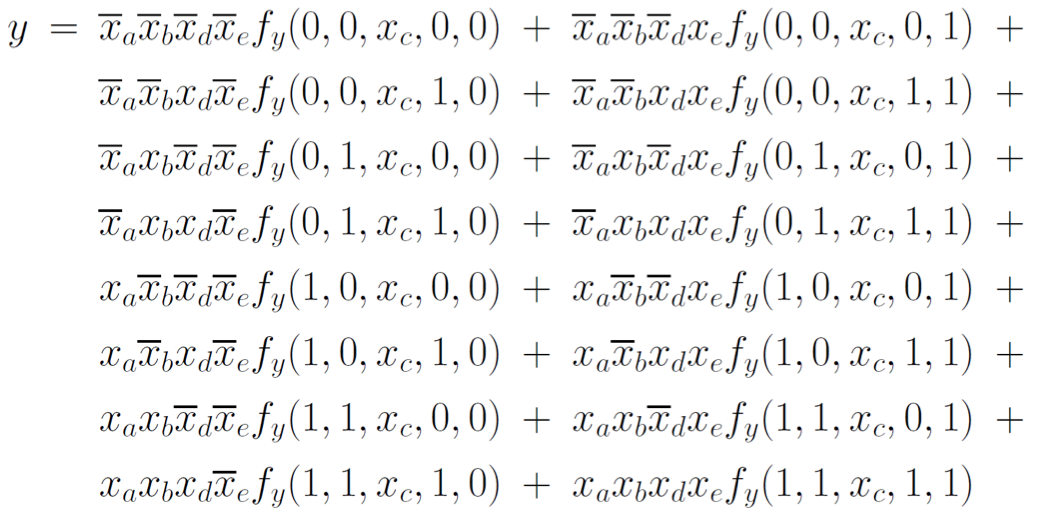
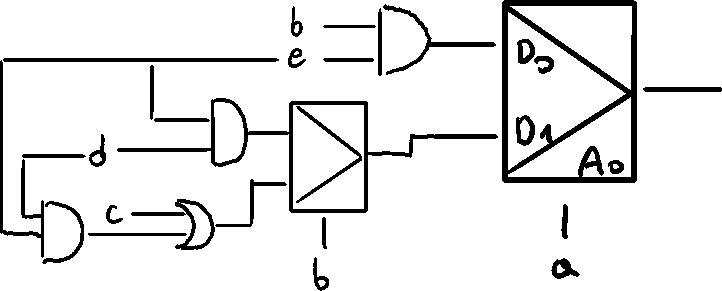
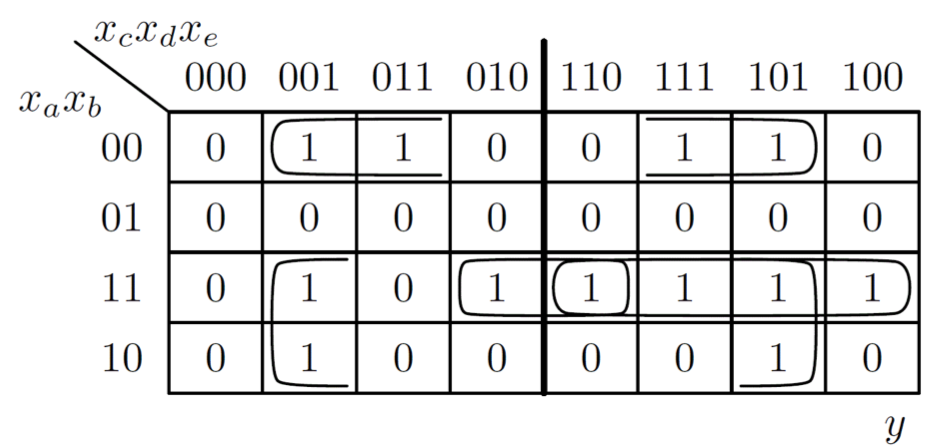
Example 2

Most frequent variables

b and e are most frequent, as they appear in every Y product
This means, we can use those inputs as select lines (addr. input)

Function for each MUX input

$b=0,e=0\to Y=\bar{b}\bar{e}=1\to I_1=1$
$b=1,e=0\to Y=0+0+0=0\to I_2=0$
$b=0,e=1\to Y=0+0+0=0\to I_3=0$
$b=1,e=1\to Y=0+\bar{a}+b\to I_3=\bar{a}+b$

Decomposition

MUX decomposition is process of implementing a Boolean func for MUX
Choose some variables as MUX select lines and express function's output as function of those selections

Example

Truth table

For each combined $AB$, express f as function of C

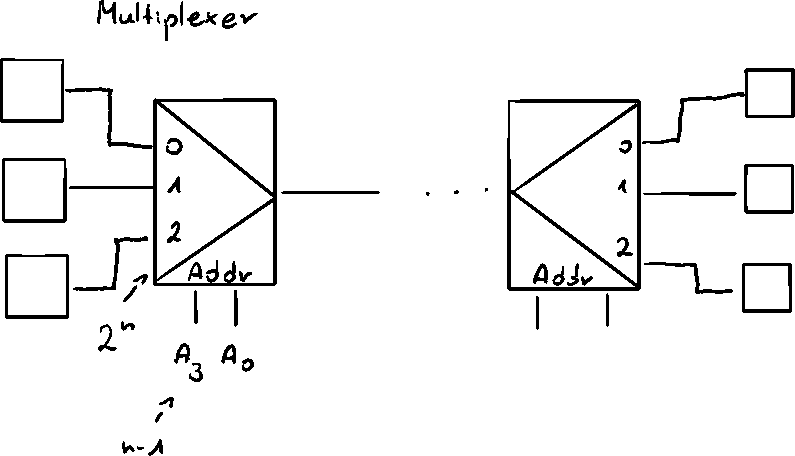
Hierarchical decomposition

Large MUX can be recursively decomposed into smaller MUXes
16:1 MUX can be build from four 4:1 MUXes and one 4:1 MUX to select among them
Any boolean func can be ultimately implemented only with 2:1 MUXes

Demultiplexer