Electrical and Computer Engineering Laboratory

Measuring process

Source of the measured quantity
Converting the measured quantity into quantity being transmitted or compared
- Sensors
- Signal converters
- Signal conditioning devices, adapters
Objective comparison system
- Comparator
- Measurand standard (reference)
Actuators - compared quantity as an observable one (display)
Information receptor (human)

Disturbances can impact any of the processes:

Noises
Environmental effects
Insertion errors
Conversion errors
Instrument errors
Data processing errors
Read-out errors

Precision vs Accuracy

Precision:

discrimination - measuring instrument reacts to small changes
repeatability - data are close in the same conditions in small period of time
reproducibility - consistent results in the case of repeating the measurement after a long period of time
Accuracy:
Measurement correctly indicates the true value of the quantity

True value ( $X_{R}$ ) - abstract notion, theoretically impossible to be determined exactly
Measurement error - quantitative expression of measurement uncertainty. algebraic difference between the measured value ( $X_{R}$ ) and the true value $X_{R} - X_{R}$

Measurement errors

Basic classification

With reference to the true value
Absolute
$Δ x = x_{M} - x_{R}$
Relative
$δ x = \frac{Δ x}{x_{R}} = \frac{x_{M} - x_{R}}{x_{R}}$

With reference to the pattern of occurrence
Inappropriate - inaccuracy of instruments
Acquisition - interaction of instrument and measurement circuit

Residual error & measurement uncertainty

Assumption - a portion of systematic error can be determined

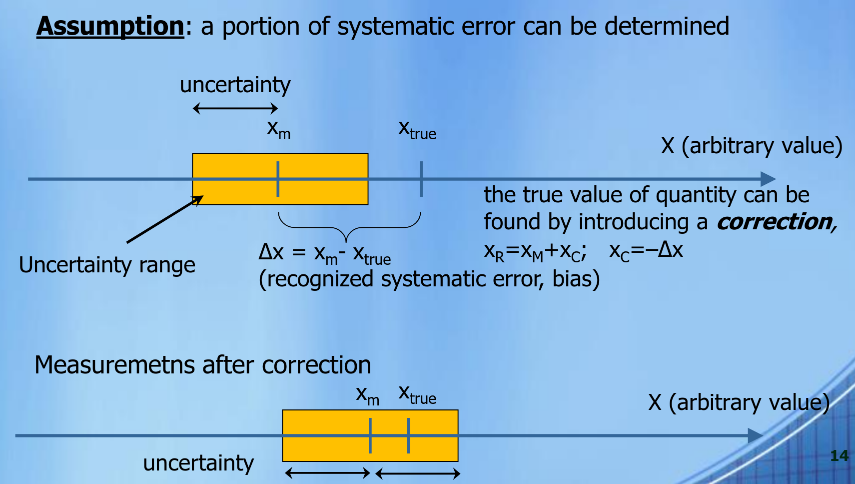
Limiting error
Assumption - interval of uncertainty is symmetric about the measured value
$Δ_{g} x$ - limiting error
One can say with extremely high probability (~100%) that the true value of a quantity lies within this interval

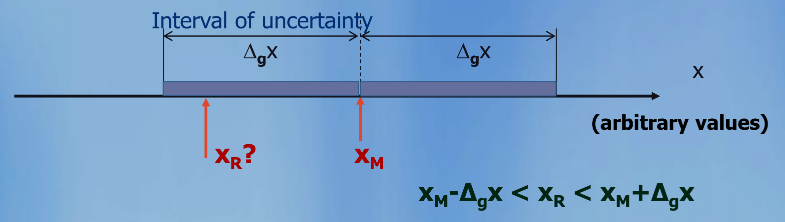
Terminology

$Δ_{g} x$ $δ_{g} x$ - limiting (absolute or relative) error of x
$u (x)$ - standard uncertainty of a quantity x
$u (\bar{x})$ - standard uncertainty for mean value
$u_{r e l} (x) = u_{r} x = \frac{u (x)}{x}$ - standard relative uncertainty
$u_{c} (y)$ - combined uncertainty
$U (x) = k \cdot u_{c} (x)$ - expanded uncertainty (k - coverage factor 1, 2, 3)

Uncertainty

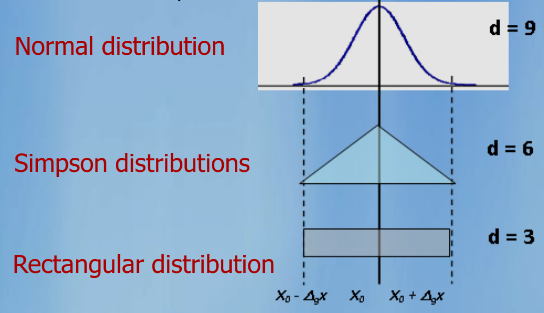
Type A

calculated from series of repeated observations (n>=4)
Mean value $\bar{x} = \frac{\sum_{i = 1}^{n} x_{i}}{n}$
Standard deviation of single measurement $u (x) = S_{x} = \sqrt{\frac{1}{n - 1} \sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}}$
Standard deviation of a series of measurements $u (\bar{x}) = S_{\bar{x}} = \frac{S_{x}}{\sqrt{n}} = \sqrt{\frac{\sum_{i = 1}^{n} (x_{i} - \bar{x})^{2}}{n (n - 1)}}$

Type B

evaluation of uncertainty by means other than the statistical analysis of series of observations

u_{b} (x) = \frac{δ_{g} x}{\sqrt{d}}

$δ_{g} x = k \cdot u (x)$ - expanded uncertainty

u_{c} (z) = \sqrt{u^{2} (x) + u^{2} (y)}

Significant figures

Nonzero integers always count as significant figures
$1653$ - 4 sign. figures
Leading zeros do not count as significant figures
$0.0345$ - 3 sign. figures
Captive zeros - always count as sign. figures
$17.04$ - 4 sign. figures
Training zeros - significant ony if the number contains a decimal point
$3.600$ - 4 sign. figures
$1.0070$ - 5 sign. figures
$14.60$ - 4 sign. figures
$100740$ - 5 sign. figures
$4.76 \cdot 10^{3}$ - 3 sign. figures
$0.00074$ - 2 sign. figures
$4600000$ - 2 sign. figures
$4.76 \cdot 10^{3}$ - 3 sign. figures

Mathematical operations

Multiplication and division - sign. figures in the result equal the number in the least precise measurement used in the calculation
$6.38 \cdot 2.0 = 12.76 \to 13$ - 2 sign. figures
$100.0 / 23.7 = 4.219409 \dots \to 4.22$ - 3 sign. figures

Addition and subtraction - number of decimal places in the result equals the number of dec. placesin the least precise measurement
$6.8 + 11.934 = 18.734 \to 18.7$ - 1 dec. pl., 3 sign. figs
$0.02 + 2.371 = 2.391 \to 2.39$ - 2 dec, 3 sign. figs.

GENERALLY uncertainties should be rounded to one (max two)significant figures
The latest sign. fig. in any stated answers should be of the same order of magnitude (in the same dec. position) as the uncertainty

Writing results

$\hat{y} \pm u (y)$	$\hat{y} \pm u_{r e l} (y)$
$\hat{y} \pm Δ_{g} \hat{y}$	$\hat{y} \pm \frac{Δ_{g} \hat{y}}{\hat{y}} \cdot_{100 %}$
$23 \pm 2 k g$	$23 \pm 9 %$
$0.879 \pm 0.015 A$	$0.879 A \pm 1.7 %$

Instrument error (accuracy)

Class index of an instrument is the lowest number from the series $c l ϵ {\dots 0.1; 0.2; 0.5; \dots}$ which meets the inequality

c l \geq \frac{| Δ x |_{m a x}}{x_{m a x} - x_{m i n}} \cdot 100 %

where
$x_{m a x} - x_{m i n}$ - range of instrument
$Δ x_{m a x}$ - maximum (absolute) error in this range
This applies for analog read instrument

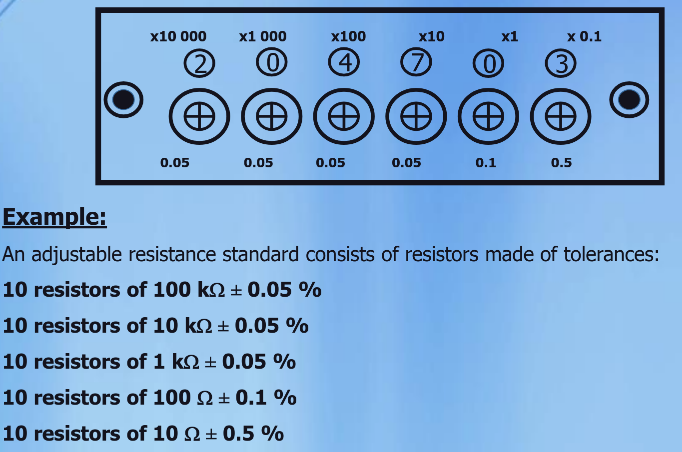
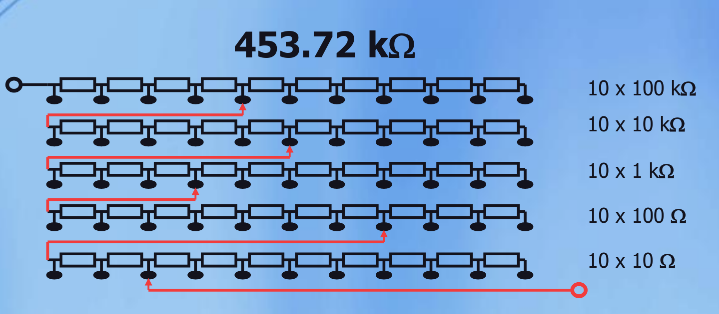
Example for a decade box

Δ_{g} R = 4 \cdot 100 k Ω \cdot 0.0005 + 5 \cdot 10 k Ω \cdot 0.0005 + \dots + 2 \cdot 0.01 k Ω \cdot 0.005 = 0.2273 k Ω = 0.23 k Ω

R = (453.72 \pm 0.23) k Ω

δ_{g} R = \frac{Δ_{g} R}{R} = \frac{0.2273}{453.82} = 0.000501 = 0.05 %

Digital read-out

Δ_{g} U = a \cdot U + b \cdot U_{F S}

where:

b - zero error
a - full scale error

Alternative definition:

δ_{g} U = a + b \cdot \frac{U_{F S}}{U}

Precision of digital read-out

174.358V - Precision of the result $\pm 0.001 V = \pm 1 m V$
It is precision not accuracy of the measurement

Fundamental formulae

When the result of measurement depends on one variable only

y = f (a)

Δ y = \frac{\partial f}{\partial a} |_{a = a_{M}}

Absolute error - $Δ x = x_{M} - x_{R}$
Relative error - $δ x = \frac{x_{M} - x_{R}}{x_{R}}$

Error summation law

y = f (x_{1}, x_{2}, \dots, x_{n})

Δ_{g} y = \sum_{i = 1}^{n} | \frac{\partial f}{\partial x_{i}} |_{0} Δ_{g} x_{i}

u (y) = \sqrt{\sum_{i = 1}^{n} (\frac{\partial f}{\partial x_{i}})^{2} \cdot u^{2} (x_{i})}

$x_{1}, \dots, x_{n}$ - values obtained from direct measurements of quantities $X_{1}, \dots X_{n}$
$y$ - value of quantity Y determined indirectly
$Δ_{g} x, Δ_{g} y$ - limiting errors of variables x and y
The symbol $| |_{0}$ denotes absolute value of parial dericative calculated for measured (indicated) values of x